| 简单电阻比较器电路形成鲁棒的Hopfield神经网络ADC Hopfield网络可以将模拟信号转换成数字形式,实现联想记忆、信号估计和组合 优化,类似于人类视网膜实现第一极信号处理的方法。本设计方案探究了Hopfield神经网络ADC的范例。 简单的转换器由一层神经元组成,其接收模拟输入,并产生数字位输出;这样的神经元构成了一种自适应和分布性的处理网络。这些神经元由电压比较器组成,驱动模拟转换器或跟随器,从转换器或比较器的模拟输出到跟随器之间连接反馈电阻(图1和图2)。参考和模拟输入电压驱动神经网络,数字输出来源于网络中的比较器。Hopfield网络具有学习能力;本设计方案的电路采用不同的自适应学习规则,通过使用可选的比较器-转换器/比较器-跟随器方案,电导节点规划方案——反馈电阻的倒数——在输入比较器之间,和位顺序读出器。 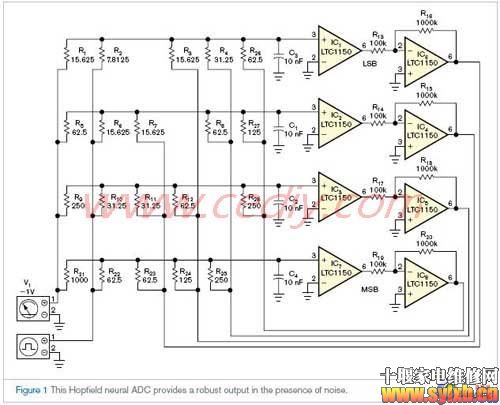 javascript:if(this.width>500)this.style.width=500;" border="0" /> javascript:if(this.width>500)this.style.width=500;" border="0" />
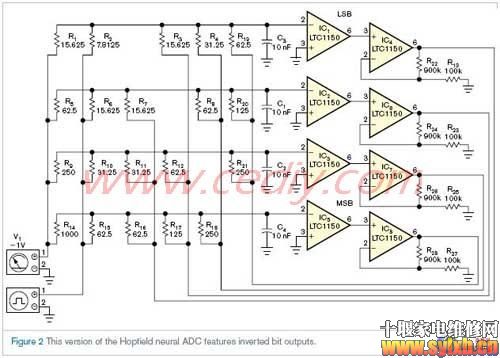 javascript:if(this.width>500)this.style.width=500;" border="0" /> javascript:if(this.width>500)this.style.width=500;" border="0" />
随着模拟输入电压的增加,电路产生单调增加(比较器-转换器方案)或减少(比较器-跟随器方案)位-字输出。减少输出是增加输出的补码,建议使用有负号的位践作。此外,形成转换器到模拟输入电压的数字响应,在不同程度上使用不同的电导节点规划作为 规则适应的一部分。为了更多的适应性,颠倒数字读出器的位顺序考虑模拟输入/数字输出特性的电路响应映射。 简单的声明一些符号和含义来构造两个转换器。对能量函数,有抵抗力的网络电导——神经键的权重(S)以倒数电阻的形式(R)——定义SIJ=1/RIJ,在此I 为第I 级的输入比较器,J 为第J 级到第I 级比较器的反馈路径,I 不等于J ——也就是说,没有比较器的自反馈路径。第I 级比较器的输入终端和参考电压VR之间的电导,定义为SIR=1/RIR。第I 级比较器的输入终端和模拟输入信号电压VS的电导,定义为SIS=1/RIS。 对绘曲线装置,Y为规一化输出位变量,X为非零平均值(小于1)到1的规一化输入模拟电压。A、B和C为用曲线方程Y=1–A×(1–X)C拟合的常数,补充曲线方程Y=A×(1–X)C,在此,A为系数,B为X的较低限制,且小于1,C为功率常数。对位格式读出器反转,有曲线方程Y=A×(X–B)C和补充曲线方程Y=1–A×(X–B)C。 图1显示了一个使用比较器驱动电压转换器的4位神经网络ADC。比较器的正端连接到输入节点,负端接地。这个网络的基础是一半的反转因数——也就是说,两个倒数因数——输入节点的电导SIJ=–1×2(2–I–J),在此,–1的参数来自相关电阻的负反馈;SIR=2(1–2×I);和SIS=2(1–I)。为确定节点电阻,选择 大节点电阻为1000Ω,相应的 小电导为0.0078125,而 小节点电阻7.8125Ω,相应的 大电导为1。按电导和终端之间的比例计算所有电阻。使用这些值,可以构造表1。表中列出了范围从 重要到 次要的位。表格显示的数字化过程不准确,因为其不是线性的,造成输入电压和许多中间位字的丢失。但是过程是精确的,因为其在相当大的输入电压范围内是可重复的。从表格可以得到下面的曲线拟合方程: Y=1–1.6243×(1–X)3.1508。当X覆盖归一化的0.1427到1范围,A=1.6243,B=0.1427和C=3.1508。Y方程实际上为三次方,其数量上显示出数字化过程的高度非线性特性。可以获得“错乱”的映射——也就是说,不是一个真正的反映,或假的——从电路通过反转位顺序读出器,归一化图形上直线曲线的版本,所以曲线方程结果为:Y=1.6243×(X–0.1427)3.1508。 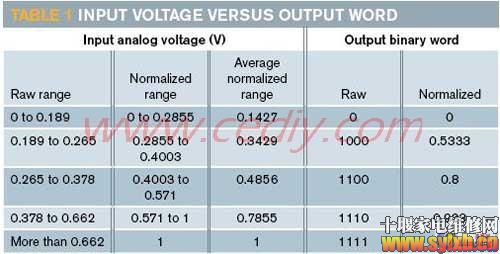 javascript:if(this.width>500)this.style.width=500;" border="0" /> javascript:if(this.width>500)this.style.width=500;" border="0" />
没有模拟输入电压转换,例如使用查询表格或对数放大器处理输入电压,或数字校准逻辑,简单Hopfield神经网络转换器的数字响应为非线性和粗略。然而,由于输出精度的鲁棒性,这些响应仍可能对结合存储器和模式分类的应用有效。 确实,由于输出数字的稳定性,Hopfield神经转换器引入了不需要的模拟输入信号噪声或变化。这个情形与传统模拟传输媒介和数字计算装置之间的接口电路形成了强烈的对比。本设计方案显示了灵活的电路适应性从神经网络ADC产生各种形式的稳定数字输出,取决于神经网络信号处理的设计人员需求。这种适应性有各种输入节点电导规划的形式;比较器/转换器和比较器/跟随器结合;位读出器的可选顺序类型源于比较器。
|
