电力系统短期负荷预测的模糊神经网络方法
姜 勇 卢 毅 东南大学（南京210096）
摘 要 针对电力系统短期负荷预测问题，考虑到气象因素对负荷的影响，提出了一种模糊神经网络的短期负荷预测方法，首先根据评价函数选取相似日学习样本，然后利用隶属函数对影响负荷的特征因素向量的分量进行模糊处理，采用反向传播算法，对24点每点建立一个预测模型，提高了学习效能。本方法适合在短期负荷预测中使用，具有较好的预测精度。
关键词 短期负荷预测 隶属函数 人工神经网络
0 引 言
短期负荷预报是电力系统管理现代化的重要内容之一，是对发电、输电和电能分配等合理介绍的必要前提，对提高电力系统的经济效益和社会效益，保障电力系统的安全经济运行与国民经济的发展具有非常重要的影响。因此，寻求有效的负荷预报方法，提高预测结果的准确度具有重要意义。
传统的预测模型是用显式的数学表达式加以描述，这就决定了它的局限性。事实上，电力负荷变化受天气情况和人们的社会活动等因素的强烈影响，存在大量非线性关系，其发展规律很难用一个显式的数学公式予以表示。因此，将具备模糊数据处理能力的模糊理论与擅长拟合非线性映射的神经网络方法结合起来，是一种比较有效的预测技术。
1 模糊理论与人工神经网络方法简介〔1，2〕
模糊神经网络是通过将模糊理论和人工神经网络理论有机结合来实现的，常见的结合方式有：a．仍采用普通神经网络的结构，但将普通非线性神经元用模糊运算神经元代替；b．采用普通神经网络的结构和神经元作为信息处理工具，而网络的输入量、输出量等则采用输入、输出信息的模糊隶属度。本文采用的模糊神经网络为后一种类型，即将输入量经过隶属度函数转化为模糊量后，再交给神经网络进行处理，以提高负荷预报的精度。
1．1 模糊集合论的概念
客观事物的差异在中介过渡时所呈现的亦此亦彼的现象称为模糊性，它体现了事物变化的连续过程。模糊集合论使用隶属度来描述中介过渡，是以精确的数学语言对模糊性的一种表述。
设论域u＝｛x｝，u到闭区间〔0，1〕的任一映射uA（x）∶u→〔0，1〕，x→uA（x）确定了u的一个模糊子集，简称模糊集，记作A，该映射称为A的隶属函数。uA（x）的大小反映了x对模糊集A的隶属程度，简称为隶属度。实数集合上常用的隶属函数为F分布，主要有矩形分布，梯形分布，抛物形分布等，在实际应用中可根据对象特点加以选择。
1．2 人工神经网络和反向传播算法的原理
神经网络是由处理单元组成的一种并行、分布式信息处理结构，处理单元之间由单向信道相互连接。人工神经元是神经网络的基本计算单元，模拟了人脑中神经元的基本特征，一般是多输入／单输出的非线性单元，可以有一定的内部状态和阈值。
反向传播（Error Back Propagation－BP）算法是多层感知器的一种有效学习算法，它的模型为前向多层网络，如图1所示。
网络不仅有输入层节点、输出层节点，而且有隐含层节点，经过作用函数后，再把隐节点的输出信息传播到输出节点， 后给出结果。节点的作用函数通常选取s型函数，如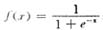
这个算法的学习过程由正向传播和反向传播组成。在正向传播过程中，输入信号从输入层经隐含层逐层处理，并传向输出层，每一层神经元的状态只影响下一层神经元的状态。如果在输出层不能得到期望的输出，则转向反向传播，将误差信号沿原来的连接通道返回，通过修改各层神经元的权值，使得误差信号 小。
BP算法可描述为：
a．权值和阈值初始化：随机地给全部权值和神经元的阈值赋以较小的初始值；
b．给定输入xk和目标输出yk；
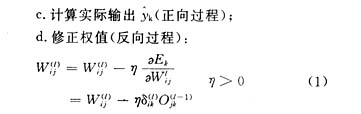
其中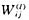
为第l层第j个神经元到第l＋1层的第i个神经元的权系数，η为增益项，δ（l）ik为第l层i节点的k模式的误差项，且有
若i为输出节点，则
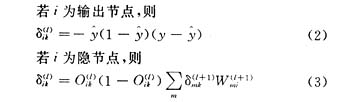
e．达到误差精度要求则输出结果，否则回到3。
2 预测方法〔3〕
2．1 BP网络学习样本的选择
根据差异评价函数选择一批比较相似的负荷日，选择方法如下：
a．首先将影响因素向量的各分量数值化，这些因素包括日类型，工作日取1，双休日取2；光照，晴天取1，少云取2，多云取3，阴天取4，下雨取5；雨量，无雨取0，小雨取1，中雨取2，大雨取3，暴雨取4； 高温度、 低温度、平均温度等可取实际值。
b．建立评价函数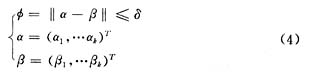 
其中是α－β的范数，α为已知日的影响因素向量，β为预测日的影响因素向量（预测值），δ为设定的偏离值，要根据不同地区的实际情况由经验决定。凡是满足该评价函数的已知日均可加入学习样本。
2．2 预测方法
为了提高BP网络的学习速度和预测精度，对网络输出的实际负荷值进行规一化处理，同时使用隶属度函数对输入网络的影响因素向量进行模糊化处理，使得输入向量的不同分量如工作日、光照、雨量、温度等都转换为模糊量。
日类型的隶属度函数采用半矩形分布，形式如下。
对工作日的隶属度函数为：
温度的隶属度函数分别如下。
对低温的隶属度函数采用偏小型梯形分布：
对中温的隶属度函数采用中间型梯形分布：
对高温的隶属度函数采用偏大型梯形分布：
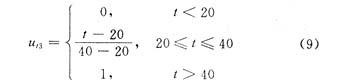
将 高温度th代入以上3个公式，可分别求出对于低温、中温、高温3个状态的隶属度。对于 低温度t1、平均温度tα，可采用同样方法求出它们的3个状态隶属度。
影响因素向量的其它分量如光照、雨量等的隶属度函数与温度相似，根据当地实际情况选择建立相应的分布函数，从而求出光照的5个状态隶属度以及雨量的5个状态隶属度。
另外，为了降低求解规模，对1d的24点负荷每点建立1个预测模型，第i点的输入输出函数为：
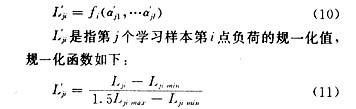
其中Lji是指第j个学习样本第i点负荷的实际值，Ljimin是学习样本中第i点负荷的 小值，Ljimax是学习样本中第i点负荷的 大值，经过规一化处理后，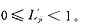
fi是指第i点的输入输出函数，α′j1，…α′jl是第j个样本影响因素的隶属度向量，包括2个代表日类型的隶属度，3个代表 高温度的隶属度，3个代表 低温度的隶属度，3个代表平均温度的隶属度，5个代表光照的隶属度，5个代表雨量的隶属度。当学习完成后，将预测日当天影响因素的隶属度向量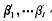
代入（10）式，则可得第i点的负荷预测值。
2．3 一些注意事项
a．伪数据的处理
因为神经网络所用的负荷数据来自电力部门的SCADA系统，由于各种原因会造成一定数量的异常数据。考虑到负荷前后小时的自然变化，如果出现超常规值，必须将其剔除，代之以正常比例范围内的估计值。
b．待选的相似日范围
因为随着时间的推移，系统负荷结构会发生缓慢的变化，当已知日和预测日相隔较远时，即使它们的天气情况等因素很相似，预测精度也不会高，因而取前3个星期的已知日作为待选范围，同时还可以缩短程序选取样本所花费的时间。
3 计算实例分析与结论
3．1 实例计算
对南京市某日24点的负荷进行预测，所得结果如表1。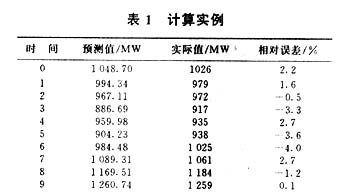 
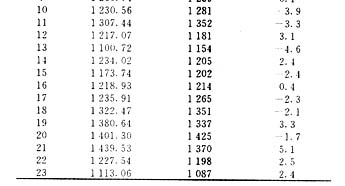
预测的平均绝对百分误差为2．56％， 大预测误差为5．1％， 小误差为0．1％，误差超过5％的预测点有1个，小于3％的点有15个，预测效果良好。
3．2 结 论
准确进行短期负荷预测是电力行业所企盼的，本文提出一种模糊神经网络预测方法，利用模糊技术和神经网络各自的特长，充分发挥了ANN处理非线性问题的能力，具有训练速度快，学习精度高，数值稳定等优点，算例也表明这是一种行之有效的短期日负荷预测方法。 参考文献
1 杨纶标，高英仪．模糊数学原理及应用．华南理工大学出版社．2001，3
2 胡守仁，余少波，戴葵．神经网络导论．长沙．国防科技大学出版社．1993，10
3 牛东晓，曹树华，赵磊，张文文．电力负荷预测技术及其应用．北京．中国电力出版社．1998，10
您当前的位置：
